数据结构:二叉树
二叉树的特点
- 二叉树中每个节点最多有两棵子树,称为左子树、右子树;
- 左子树和右子树是有顺序的,有左右之分,次序不能随意颠倒;
- 即使某个节点只有一个子树,也要区分左右子树。
即:最多两棵树,还要分左右。
- 完全二叉树:只有底层没满,且按顺序排列在左边的二叉树。
- 满二叉树:所有节点都满了的二叉树
- 二叉搜索树:节点分大小,左边>中间>右边。
- 平衡二叉树:左右子树的高度差最大为1。
- 平衡二叉搜索树:集合二叉搜索树和平衡二叉树两者特点的树,比如AVL树。
二叉树的存储
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
树的遍历
前序遍历
前序遍历-递归
func preOrder(t *TreeNode) {
if t == nil {
return
}
fmt.Println(t.Val)
preOrder(t.Left)
preOrder(t.Right)
}
前序遍历-非递归
中序遍历
中序遍历-递归
func inOrder(t *TreeNode) {
if t == nil {
return
}
inOrder(t.Left)
fmt.Println(t.Val)
inOrder(t.Right)
}
中序遍历-非递归
// 使用栈来记录树上的节点,栈顶的节点即是当前访问的节点
后序遍历
后序遍历-递归
func postOrder(t *TreeNode) {
if t == nil {
return
}
postOrder(t.Left)
postOrder(t.Right)
fmt.Println(t.Val)
}
后序遍历-非递归
DFS和BFS搜索
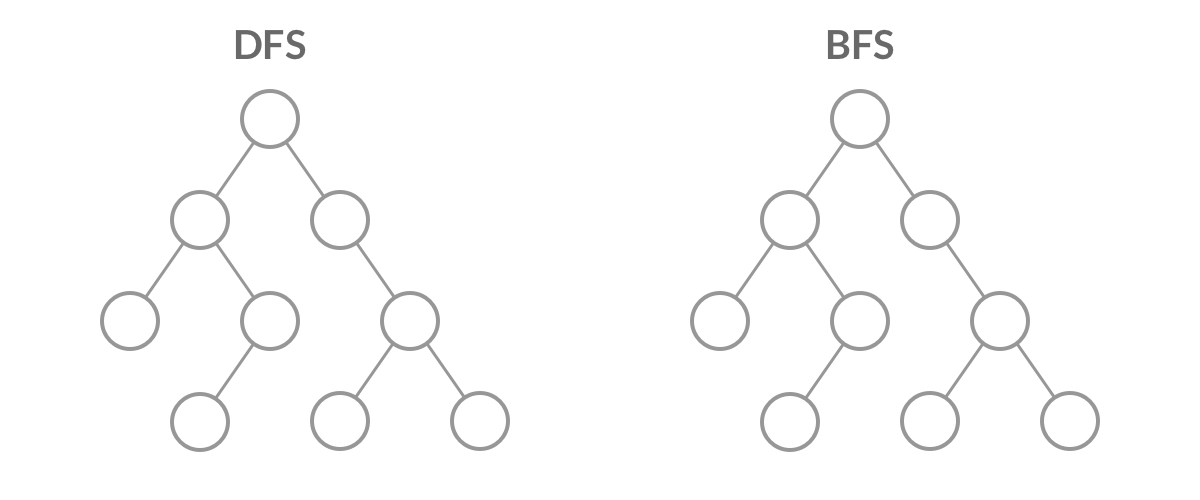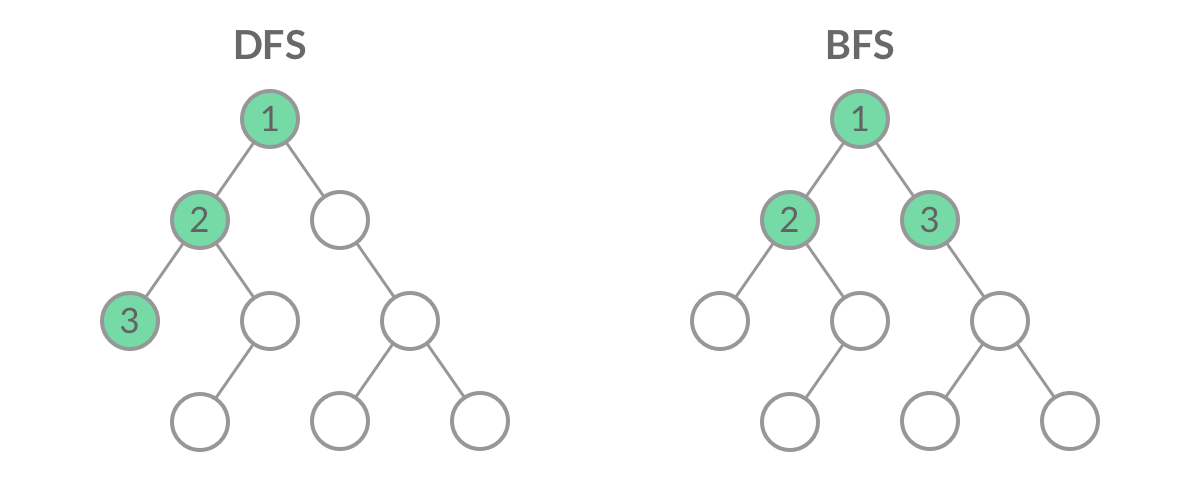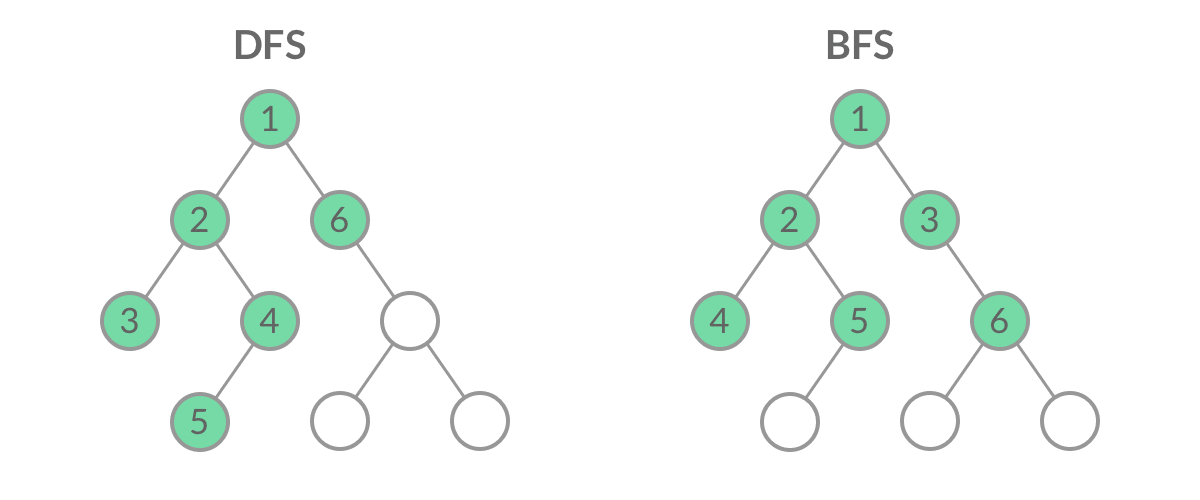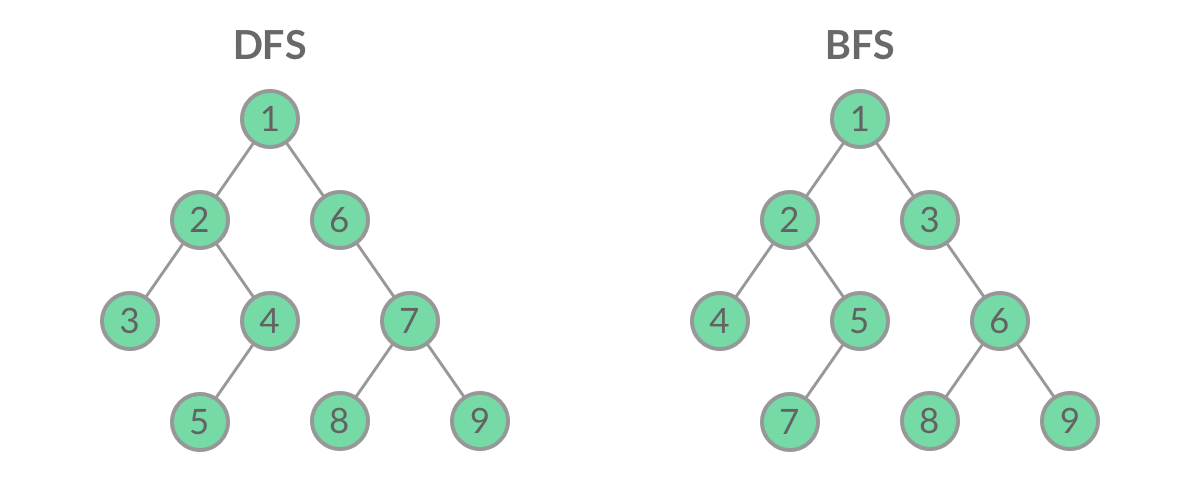
广度优先搜索(Breath First Search,BFS,又称层序遍历。一般采用队列进行遍历辅助。)
func bfs(p *TreeNode) []int {
res := make([]int, 0)
if p == nil {
return res
}
// BFS需要使用一个 **队列** 协助,此处用slice模拟队列
queue := []*TreeNode{p}
for len(queue) > 0 { //每一轮是不同层
length := len(queue)
for length > 0 { // 同层遍历
length--
if queue[0].Left != nil {
queue = append(queue, queue[0].Left)
}
if queue[0].Right != nil {
queue = append(queue, queue[0].Right)
}
res = append(res, queue[0].Val)
queue = queue[1:]
}
}
return res
}
深度优先搜索(Depth First Search,DFS。一般采用栈进行遍历辅助,可用递归来实现栈。)
func DFS(root *TreeNode) []int {
if root == nil {
return
}
var res []int
res = append(res, root.Val)
DFS(root.Left)
DFS(root.Right)
return res
}
计算二叉树的节点个数
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func countNodes(root *TreeNode) int {
if root == nil {
return 0
}
return countNodes(root.Left) + countNodes(root.Right) + 1
}
计算二叉树的深度
func maxDepth(root *TreeNode) int {
if root == nil {
return 0
}
return 1 + max(maxDepth(root.Left), maxDepth(root.Right))
}
func max(x,y int) int {
if x > y {
return x
}
return y
}
平衡二叉树
判断一棵二叉树是否是平衡二叉树
func isBalanced(root *TreeNode) bool {
if root == nil {
return true
}
leftHeight := height(root.Left)
rightHeight := height(root.Right)
if leftHeight-rightHeight < -1 || leftHeight-rightHeight > 1 {
return false
}
return isBalanced(root.Left) && isBalanced(root.Right)
}
func height(node *TreeNode) int {
if node == nil {
return 0
}
return 1 + max(height(node.Left), height(node.Right))
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
合并两个二叉树
func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
if root1 == nil && root2 == nil {
return nil
} else if root1 == nil {
return root2
} else if root2 == nil {
return root1
} else {
root1.Val += root2.Val
root1.Left = mergeTrees(root1.Left, root2.Left)
root1.Right = mergeTrees(root1.Right, root2.Right)
return root1
}
}
反转二叉树
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func invertTree(root *TreeNode) *TreeNode {
if root == nil {
return nil
}
left := invertTree(root.Left)
right := invertTree(root.Right)
root.Left = right
root.Right = left
return root
}
判断两棵二叉树是否相同
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func isSameTree(p *TreeNode, q *TreeNode) bool {
if (p == nil) && (q == nil) {
return true
}
if (p == nil) || (q == nil) {
return false
}
if p.Val != q.Val {
return false
}
return isSameTree(p.Left, q.Left) && isSameTree(p.Right, q.Right)
}
打印二叉树的所有路径
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
var paths []string
func binaryTreePaths(root *TreeNode) []string {
paths = []string{}
constructPaths(root, "")
return paths
}
func constructPaths(root *TreeNode, path string) {
if root != nil {
pathSB := path
pathSB += strconv.Itoa(root.Val)
if root.Left == nil && root.Right == nil {
paths = append(paths, pathSB)
} else {
pathSB += "->"
constructPaths(root.Left, pathSB)
constructPaths(root.Right, pathSB)
}
}
}
计算二叉树的最小深度
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func minDepth(root *TreeNode) int {
if root == nil {
return 0
}
if root.Left == nil {
return minDepth(root.Right) + 1
}
if root.Right == nil {
return minDepth(root.Left) + 1
}
return min(minDepth(root.Left), minDepth(root.Right)) + 1
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
二叉树的最近公共祖先
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
if root == nil {
return nil
}
if root.Val == p.Val || root.Val == q.Val {
return root
}
left := lowestCommonAncestor(root.Left, p, q)
right := lowestCommonAncestor(root.Right, p, q)
if left != nil && right != nil {
return root
}
if left == nil {
return right
}
return left
}
判断是否是轴对称的对称二叉树
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func isSymmetric(root *TreeNode) bool {
if root == nil {
return true
}
return compare(root.Left, root.Right)
}
func compare(node1 *TreeNode, node2 *TreeNode) bool {
if node1 == nil && node2 == nil {
return true
}
if node1 == nil || node2 == nil {
return false
}
if node1.Val != node2.Val {
return false
}
return compare(node1.Left, node2.Right) && compare(node1.Right, node2.Left)
}
二分搜索树(BST,Binary Search Tree)
- 二分搜索树也是一种二叉树,但二分搜索树种每个节点的值都要大于其左子树所有节点的值,小于其右子树所有节点的值;
- 每一棵子树也是二分搜索树。
验证是否是二叉搜索树
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func isValidBST(root *TreeNode) bool {
if root == nil{
return true
}
var stack []*TreeNode
cur := root
var prev *TreeNode
for len(stack)>0 || cur!=nil{
if cur!=nil{
stack = append(stack,cur)
cur = cur.Left
}else{
cur = stack[len(stack)-1]
stack = stack[:len(stack)-1]
if prev!=nil &&prev.Val >= cur.Val{
return false
}
prev = cur
cur = cur.Right
}
}
return true
}
